외로운 Nova의 작업실
비지도 학습 - 로지스틱 회귀 본문
- 로지스틱 회귀
앞서 다룬 선형 회귀 모델로 이진 분류 문제를 풀 수 있을까요? 선형 회귀의 예측값은 수치값으로 나와서 참 또는 거짓을 분류하는 문제에 적합하지 않습니다. 단, 선형 회귀의 예측값을 입력값으로 받아 참 또는 거짓으로 분류하는 모델을 고려해볼 수 있습니다. 이번장에서 배울 로지스틱 회귀 모델은 선형 회귀를 입력으로 받아 특정 레이블로 분류하는 모델입니다.
로지스틱 회귀의 작동 원리는 다음 그림과 같습니다.

왼쪽은 선형 회귀 그래프로 x라는 입력이 들어왔을떄 wx+b라는 결과값을 출력합니다. 이 결과값이 오른쪽 그래프인 시그모이드 함수의 입력값으로 들어가 0부터 1까지의 사이값을 출력합니다. 출력값이 0.5 이상일 경우에는 참, 0.5 이하일 경우에는 거짓으로 분류하는 분류 모델로 사용할 수 있습니다. 예를 들어 아래처럼 사용할 수 있습니다.

표에서 알수 있 듯이 x값을 선형 회귀 출력값으로 변환하고 이를 로지스틱 회귀 출력값으로 변환되어 0.5를 기준으로 음수인지 양수인지 판별하고 있습니다. 즉, 로지스틱 회귀함수는 선형회귀 함수와 시그모이드 함수의 합성함수입니다.

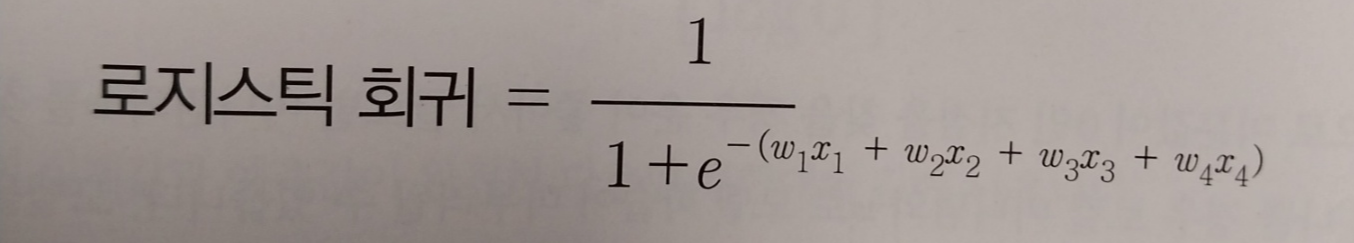
- 로지스틱 회귀 학습
로지스틱 회귀 학습이란 현재 가지고 있는 데이터를 통해 최적의 w를 찾아내는 과정입니다. 근데 이전에는 선형 회귀에서는 랜덤한 w를 최초부여한 후 경사하강법으로 평균제곱오차가 가장 작은 w를 찾아내었습니다. 로지스틱 회귀역시 경사하강법으로 최적의 w를 찾아내지만 비용함수는 평균제곱오차가 아닌 크로스 엔트로피를 사용합니다. 그 이유는 로지스틱 회귀 함수는 일차함수가 아니기 때문입니다.
일차함수가 아니다보니 평균제곱오차를 활용한 경사하강법으로 찾게되면 미분값이 0인 지점을 찾을 경우 운이 좋으면 가장 아래쪽의 글로벌 미니멈을 찾을 수도 아니라면 가장 높은 로컬 미니멈을 찾게될 수 있습니다.
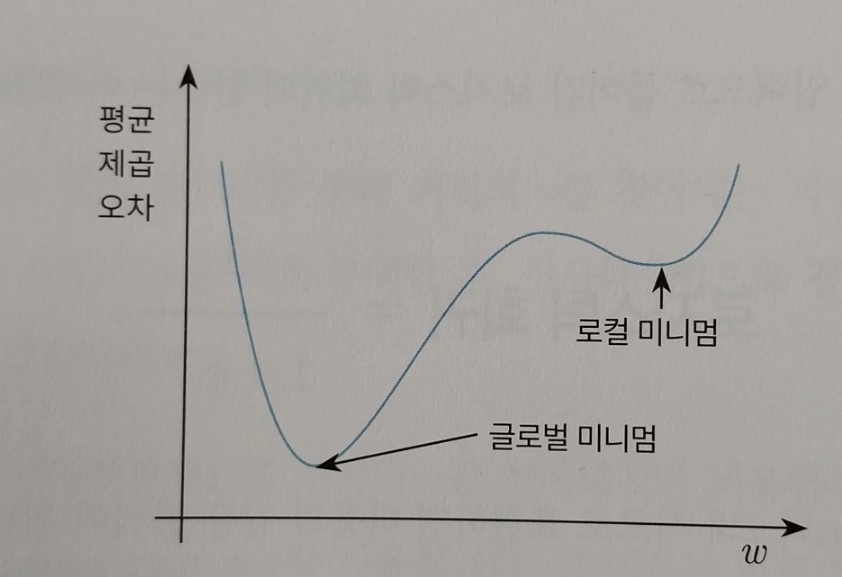
따라서 평균제곱오차가 아닌 크로스 엔트로피를 사용합니다.
- 크로스 엔트로피
크로스 엔트로피는 쉽개 모델의 예측값의 확률과 실제값의 확률의 차이입니다. 이 차이 값을 가장 작게할때 최적의 로지스틱함수를 만들 수 있을 것입니다. 따라서 이 차이를 작게하는 w를 구해야합니다.
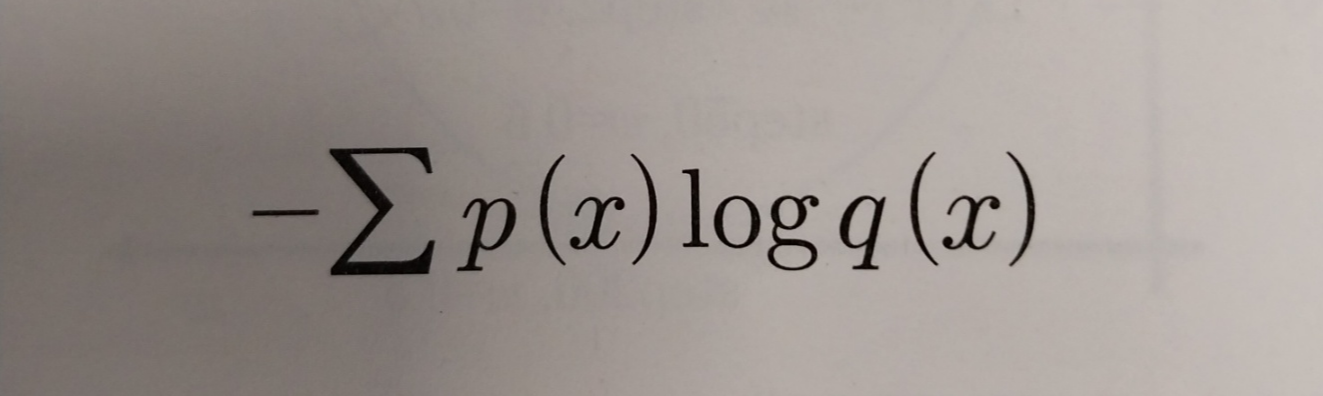
위는 크로스 엔트로피 공식입니다. p(x)가 실제데이터 q(x)가 예측값입니다. 이를 계산해보면 실제값과 예측값이 다르면 무한대 값이 나오고, 동일하다면 0이 나옵니다.
한가지 눈여겨봐야할 점은 이 크로스 엔트로피 공식을 평면상에 그려보면 아래와 같습니다.
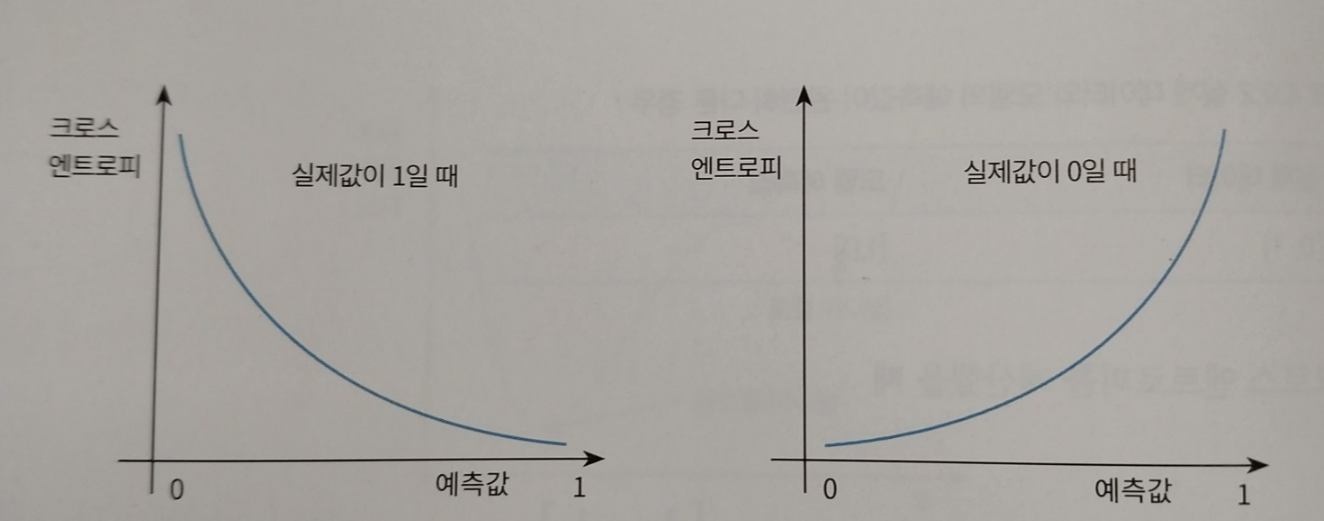
크로스 엔트로피가 가장 작을때, 즉 예측값과 동일할때의 미분값이 거의 0에 근접하다는 것입니다. 그리고 경사하강법을 사용하기 좋다는 것입니다.
- 실습 단일 입력 로지스틱 회귀
단일 입력 로지스틱 회귀는 1개의 입력으로 0과1을 구분하는 함수입니다.
from keras.models import Sequential
from keras.layers import Dense, Activation
import numpy as np
#모델 생성
model = Sequential()
model.add(Dense(input_dim=1, units = 1))
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='sgd', metrics=['binary_accuracy'])
#학습데이터생성
X = np.array([-2, -1.5, -1, 1.25, 1.62, 2])
Y = np.array([0, 0, 0, 1, 1, 1])
#학습
model.fit(X, Y, epochs=300, verbose=0)
#검증
model.predict([-2, -1.5, -1, 1.25, 1.62, 2])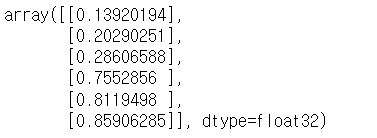
처음 3개는 음수라서 0.5보다 작고 다음 3개는 양수라서 0.5보다 큰 것을 확인할 수 있습니다.
- 실습 다중입력 로지스틱 회귀
디중 입력 로지스틱 회귀는 1개 이상의 입력으로 0과 1중하나의 값을 출력하는 함수입니다.
from keras.models import Sequential
from keras.layers import Dense, Activation
import numpy as np
#모델 생성
model = Sequential()
model.add(Dense(input_dim=2, units = 1))
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='sgd', metrics=['binary_accuracy'])
#학습 데이터 생성
X = np.array([(0,0), (0,1), (1,0), (1,1)])
Y = np.array([0, 0, 0, 1])
#모델 학습 진행
model.fit(X, Y, epochs=5000, verbose=0)
#검증
model.predict(X)
마지막 값의 y가 1이기에 0.5를 넘는 것을 볼 수 있습니다.
'AI > machine-learning' 카테고리의 다른 글
| 지도 학습 - 딥러닝 (0) | 2023.11.16 |
|---|---|
| 비지도 학습 - 주성분 분석 (0) | 2023.11.10 |
| 비지도학습 - 선형 회귀 (1) | 2023.11.06 |
| 비지도학습 - 군집화 (0) | 2023.11.04 |
| 앙상블 기법 (0) | 2023.11.03 |




