외로운 Nova의 작업실
지도 학습 - 딥러닝 본문
- 딥러닝의 탄생 배경
딥러닝은 아주 오래전에 논리적인 연산을 하기위해 만들어진 퍼셉트론에서부터 시작합니다. 퍼셉트론을 이해하면 딥러닝에대해 알아갈 수 있습니다.
- 퍼셉트론
퍼셉트론은 두개의 입력이 있을때 하나의 뉴런으로 두개의 입력을 계산한뒤 0 또는 1을 출력하는 논리적인 연산 모델입니다. 아래는 퍼셉트론의 식입니다.
z = w1x1 + w2x2 + bias(편향값)
이후 z값을 구한다음 z값에대한 활성화 함수(0과1을 구분하는 함수)로 0과 1을 출력합니다. 그림으로 설명하면 아래와 같습니다.

아래는 활성화 함수로 사용하는 스텝 함수입니다.

이렇게 0과 1을 출력하는데, and 연산에 맞는 w1,w2,bias 값과 or 연산에 맞는 w1,w2,bias의 값을 구할 수 있습니다.
예를 들어 w1 = 0.6, w2 = 0.6, bias = -1 일때 and 연산의 결과값과 일치하게됩니다.
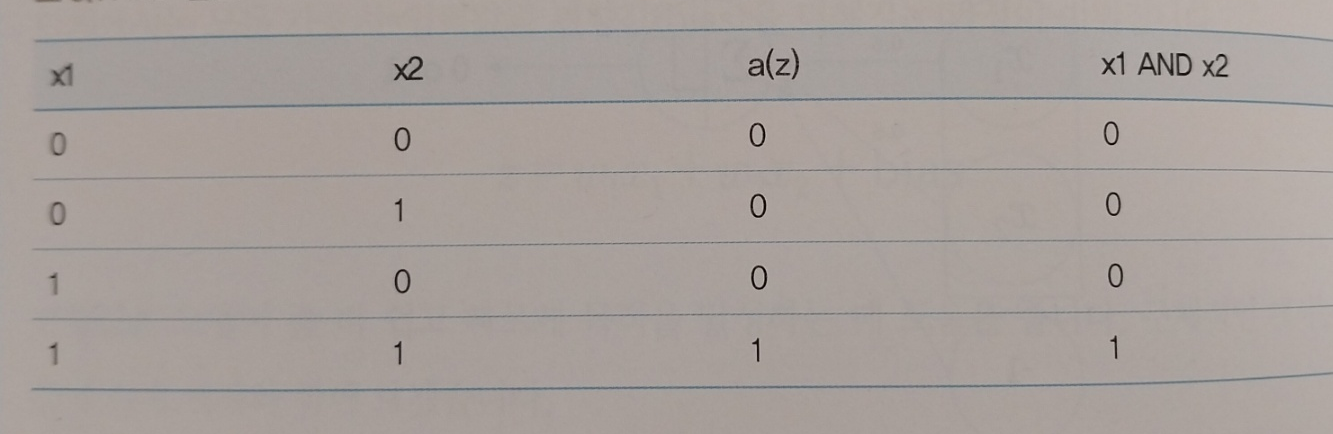
즉, 퍼셉트론의 식으로 and 연산과 or 연산을 할 수 있다는 점이 중요합니다. 하지만, 퍼셉트론은 xor 연산에 맞는 w1,w2,bias값을 구해내지 못해내지 못한다는 한계점을 가지고 있습니다. 이후 발전한게 다층 퍼셉트론입니다.
- 다층 퍼셉트론
퍼셉트론으로는 xor을 구현할 수 없었지만 두개의 퍼셉트론이면 xor을 구현할 수 있지 않을까 라고 생각해볼 수 있습니다.
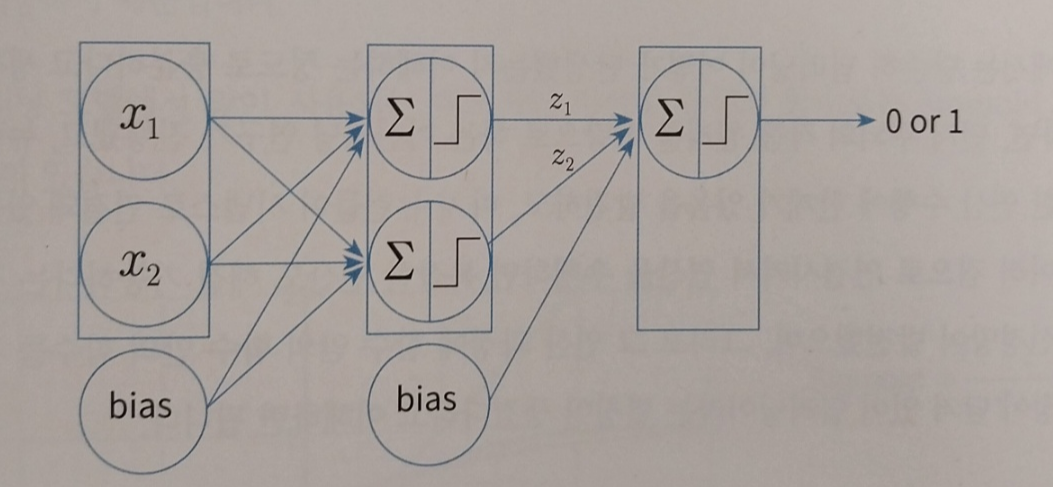
그리고 위 구조로 xor 연산을 구현해내게 됩니다. 이로서 and, or , xor, not 연산자의 논리적 결과값을 수식을 통해 구해낼 수 있게 됩니다. 여기서 알 수 있는 점은 어려운 문제를 하나씩 나누어 풀어가면 풀 수 있다는 점입니다. 이를 통해 퍼셉트론의 노드를 정말 많이 연결한 머신러닝 모델을 딥러닝이라고 하며 심층신경망이라고 합니다.
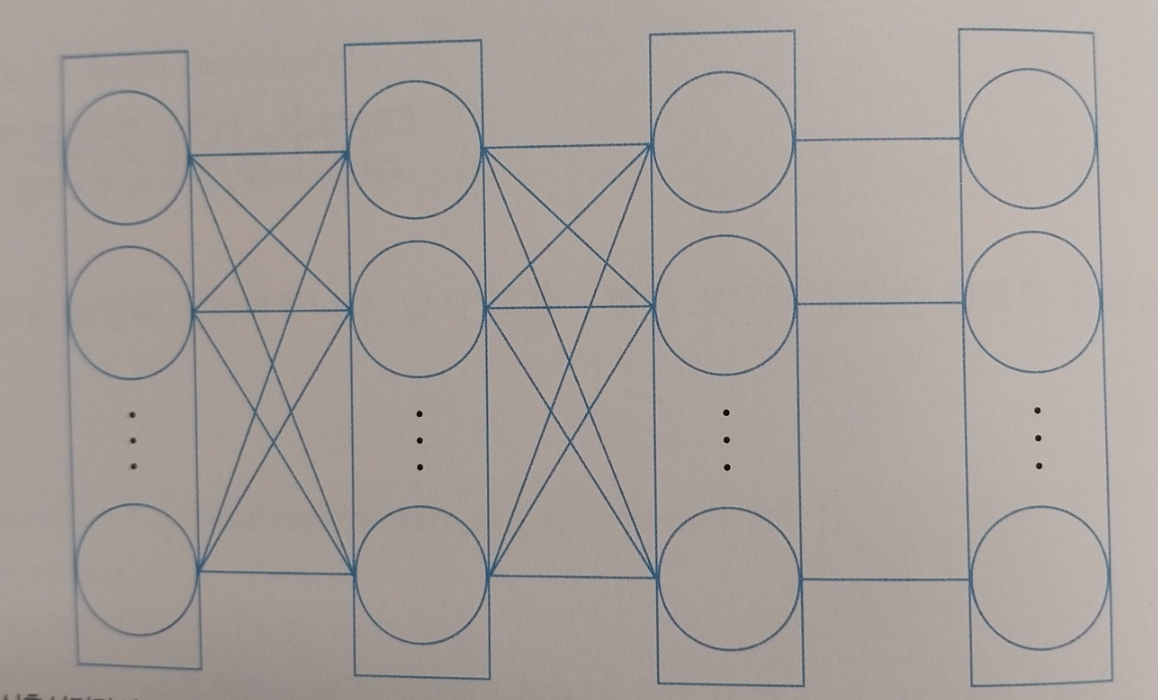
- 딥러닝의 학습
<순전파>
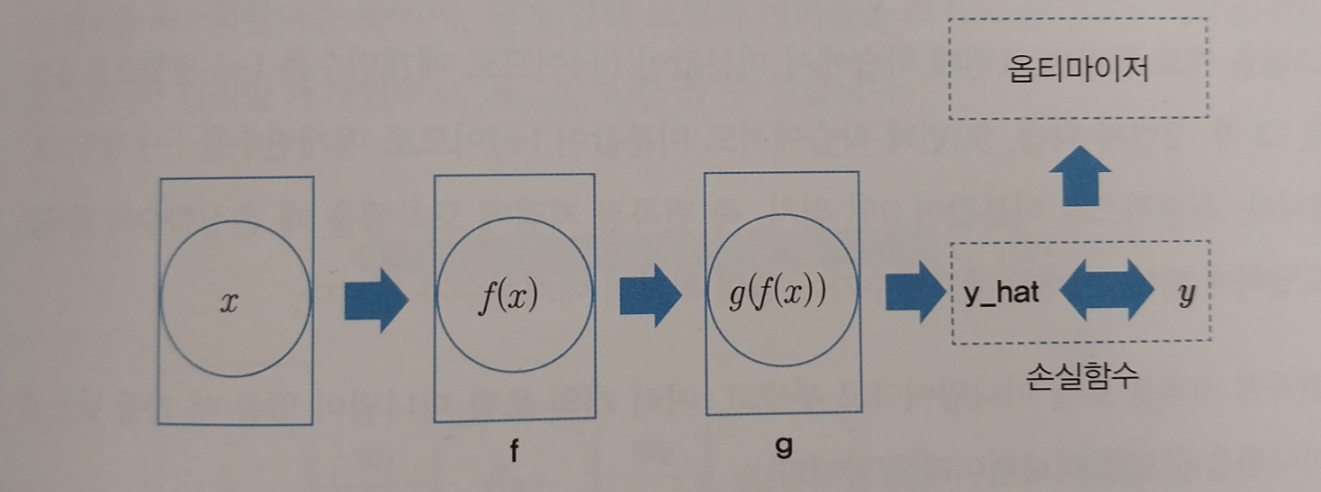
순전파란 딥러닝에 값을 입력해서 출력을 얻는 과정을 말합니다. 아래 그림처럼 왼쪽에서 오른쪽으로 데이터가 흘러가는 과정을 순전파라고 하며, 순전파에 의해 딥러닝의 출력값(y_hat)을 얻을 수 있습니다.
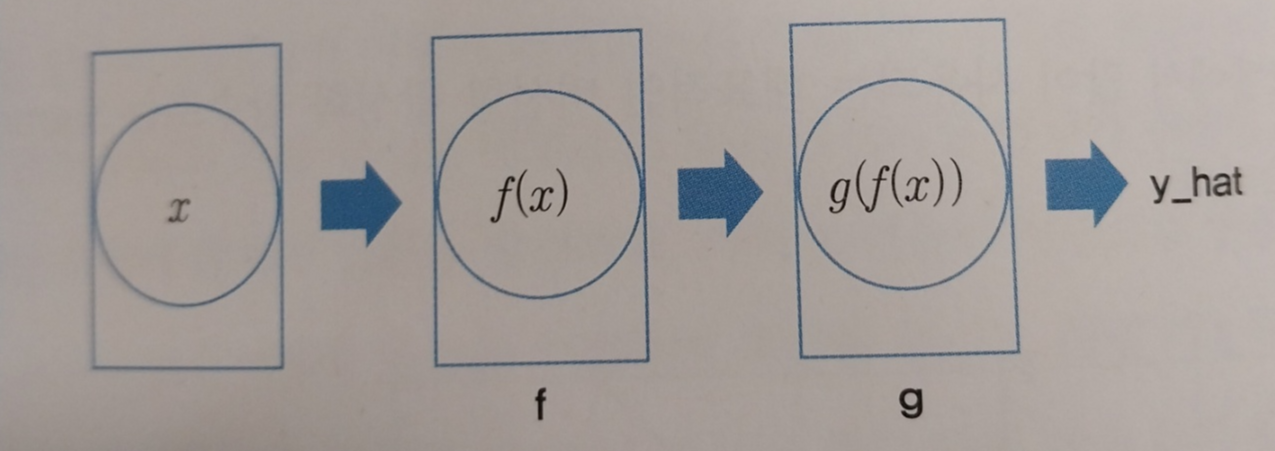
순전파 과정을 거치면 출력값을 얻게 되고 정답과 출력값의 차이를 구할 수 있게 됩니다. 출력값과 정답의 차이를 구하기 위한 함수를 손실함수라고합니다.
<손실함수>
손실함수는 출력값과 정답의 차이를 계산합니다. 출력값과 정답이 일치할 수 록 손실함수의 값은 적고, 불일치할 수 록 손실함수의 값은 큽니다. 보통 회귀에서는 평균제곱오차를, 분류문제에서는 크로스 엔트로피를 손실함수로 사용합니다. 매개변수를 조절해서 손실함수의 값을 최저로 만드는 과정을 최적화 과정이라고 부르고, 최적화 과정은 옵티마이저를 통해 이뤄집니다. 옵티마이저는 역전파 과정을 수행해서 딥러닝 모델의 매개변수를 최적화합니다.
- 옵티마이저
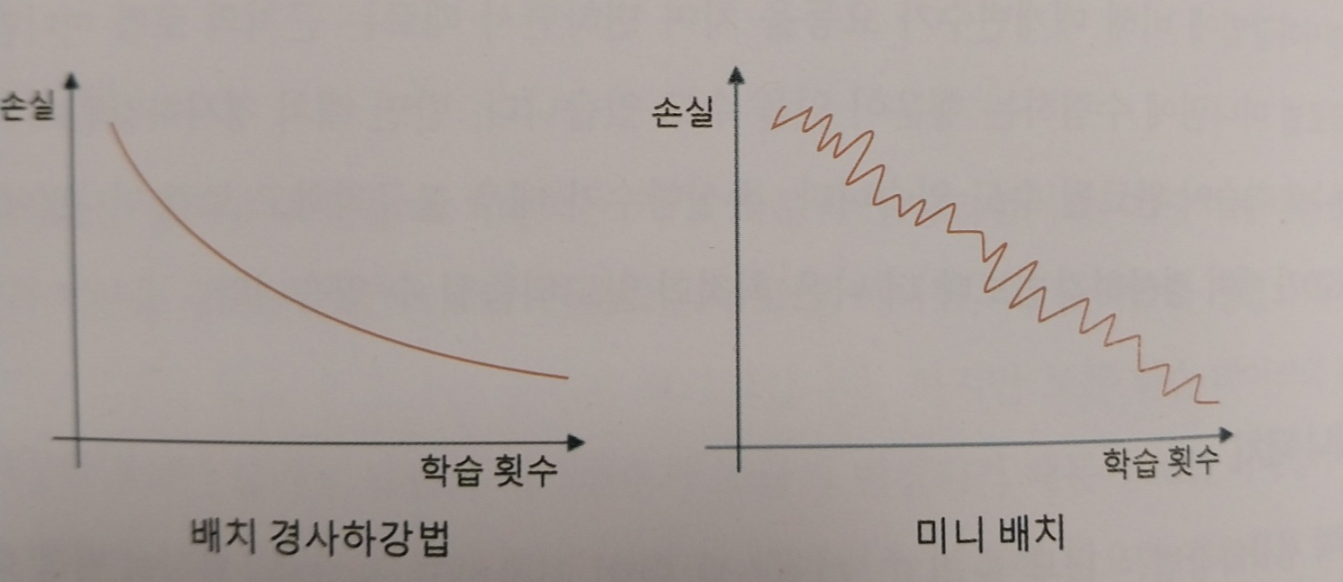
배치 경사하강법은 딥러닝 모델을 최적화하는 가장 기본적인 방법입니다. 하지만 손실함수를 계싼한 후에 매개변수가 조금씩 변경되기 떄문에 로컬 미니멈까지 매개변수를 변경하는데 걸리는 시간이 오래걸리고, 매개변수 조절에 필요한 계산량도 많다는 단점이 있습니다. 또한 로컬 미니멈은 여러개 존재할 수 있지만 경사하강법은 가장 가까운 로컬 미니멈에 멈추게될 것이라는 단점이 있습니다.
SGD는 모든 데이터를 계산해서 매개변수를 변경하는 배치 경사 하강법과 달리 하나의 데이터마다 매개변수를 변경하는 방법입니다. 비유하자면 배치 경사 하강법은 꾸준히 현재의 위치에서 최저젖ㅁ을 향해 내려가는 거북이 같다면 SGD는 껑충껑충 뛰어다니면서 최저점을 찾는 토끼와 같습니다. 제한된 자원으로 충분히 딥러닝 모델을 학습시킬 수 있다는 것이 장점입니다. 손실함수가 불규칙하고 로컬 미니멈이 많을때는 SGD가 배치 경사하강법보다 더 나은 최적화 알고리즘입니다.
미니 배치는 배치경사하강법과 SGD의 절충안으로 전체 데이터를 계산해서 배개변수를 변경하는 대신 정해진 양만큼 계산해서 매개변수를 최적화하는 방법입니다. 리소스도 적게 사용하고 학습시간도 적어서 미니 배치를 많이 사용합니다.
<학습률>
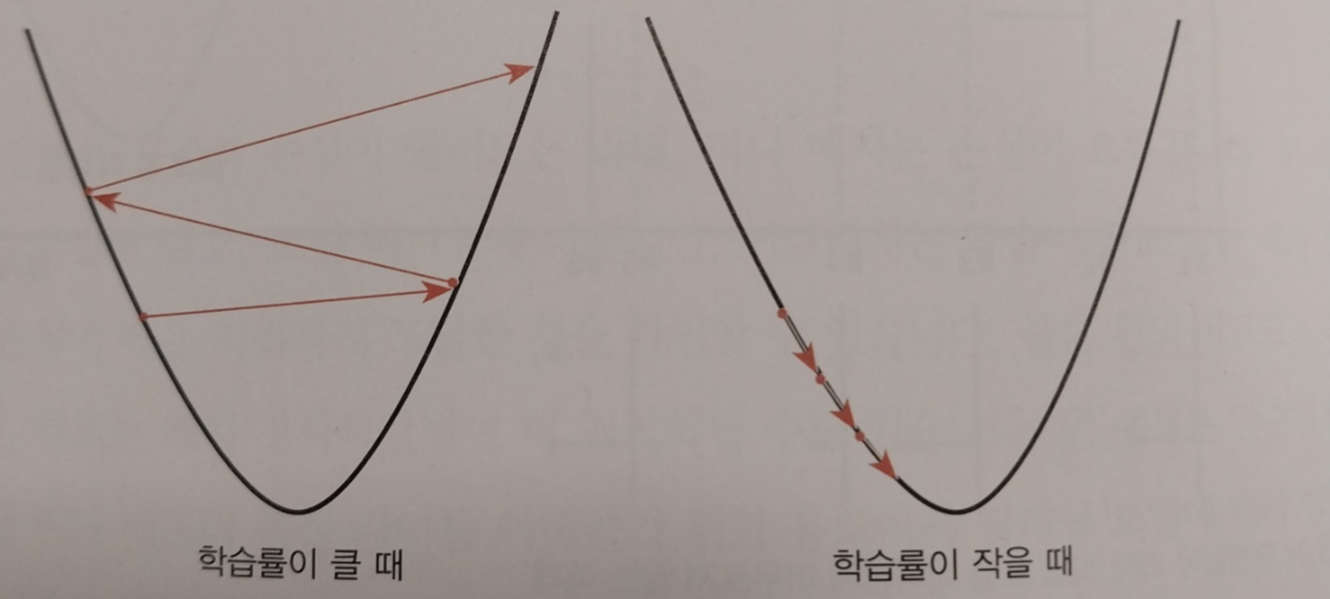
경사하강법 공식에는 항상 학습률이 있습니다. 학습률을 크게 설정하면 로컬 미니멈에 수렴하지 않을 수 있고, 또 너무 작게 설정하면 학습 시간이 상당히 오래 걸릴 수 있습니다.
- 딥러닝의 과대 적합
딥러닝 역시 지나친 학습에 의한 과대적합을 조심행먀합니다. 딥러닝 모델은 학습 시 매개변수가 상당히 많다는 점과 학습 횟수에 제한이 없으며 이 두 특이점은 딥러닝 모델에 과대적합을 볼러올 수 있습니다.
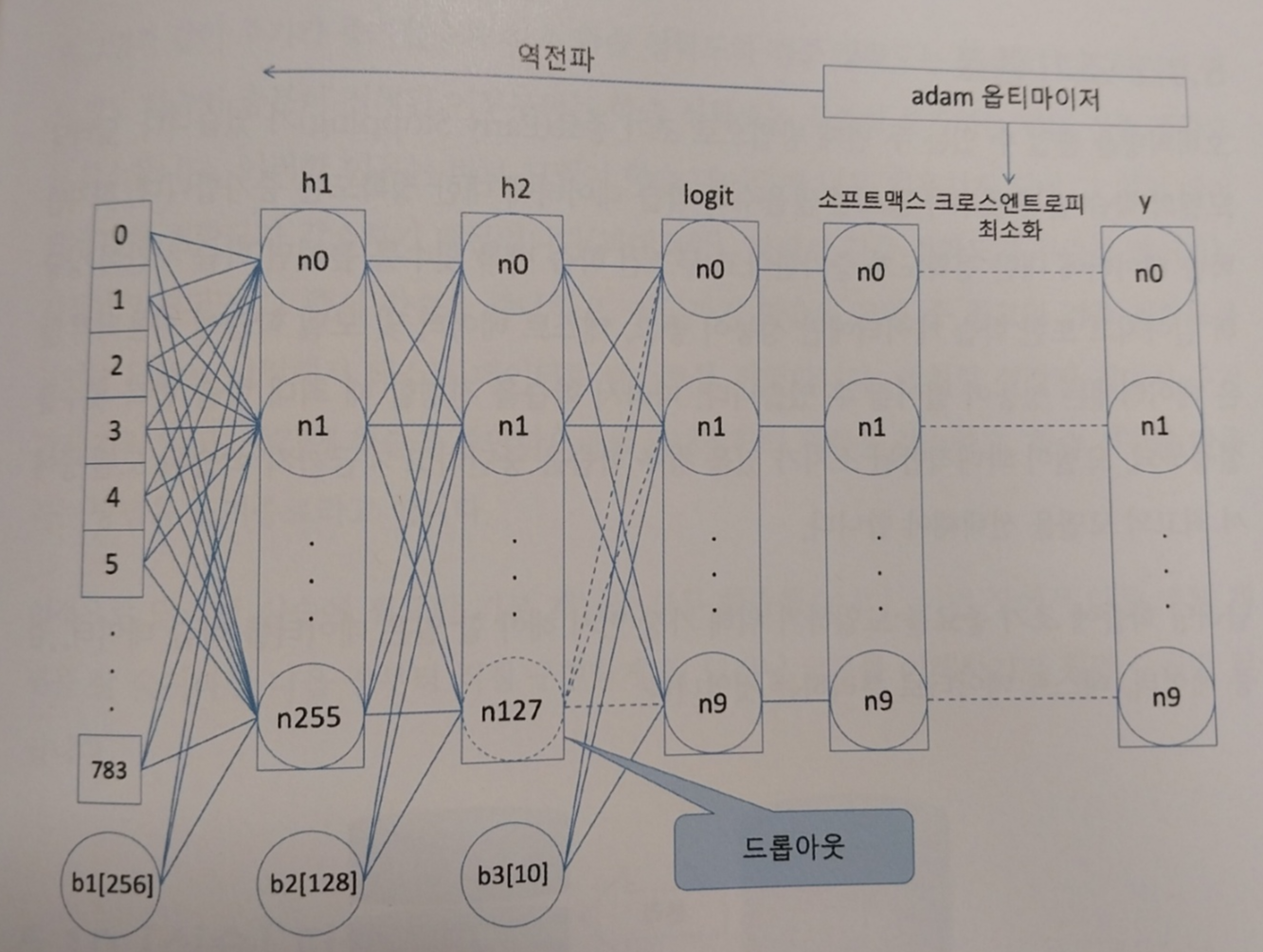
<드롭아웃>
드롭아웃은 매개변수 중 일정량을 학습 중간마다 무작위로 사용하지 않는 방법입니다. 매 스텝마다 드롭아웃이 설정된 히든 레이어에서 무작위로 선택된 노드가 학습에 사용하지 않고 매개변수가 조절됩니다. 이러한방법은 모델의 분산을 줄이는데 효과적입니다. 분산을 줄이고 편향을 높이면 과대적합 위험이 감소됩니다.
<조기 종료>
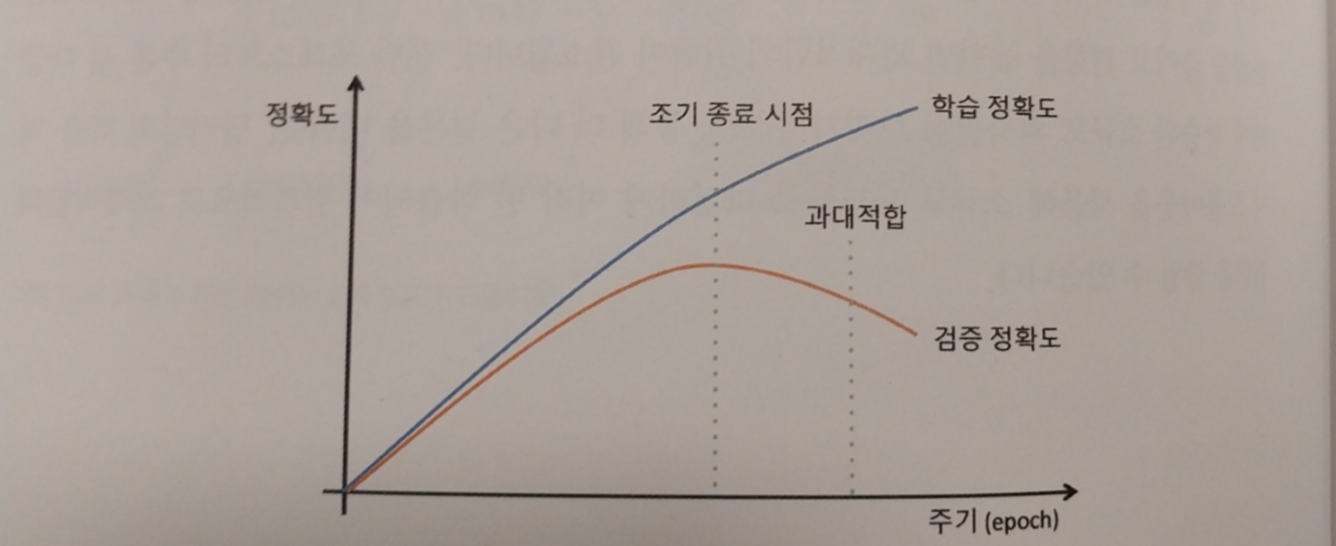
오버피팅을 줄일 수 있는 두번째 방법으로 조기 종료가 있습니다. 딥러닝 모델의 학습 반복 횟수가 많으면 많을수록 학습 데이터에 대한 정확도는 증가합니다. 하지만 무조건 학습 반복 횟수를 높이면 학습 시간이 상당히 길어지고 성능이 떨어질 수 있습니다. 따라서 최대 학습 반복 횟수를 설정하되, 과대적합될 소지가 있을 경우 학습을 중단하고 지금까지 학습된 모델 중에서 최고의 모델을 선택하는 방법입니다.
'AI > machine-learning' 카테고리의 다른 글
| 지도 학습 - 다층 퍼셉트론 실습 (1) | 2023.11.17 |
|---|---|
| 지도 학습 - 퍼셉트론 실습 (1) | 2023.11.17 |
| 비지도 학습 - 주성분 분석 (0) | 2023.11.10 |
| 비지도 학습 - 로지스틱 회귀 (0) | 2023.11.07 |
| 비지도학습 - 선형 회귀 (1) | 2023.11.06 |




