외로운 Nova의 작업실
비지도 학습 - 주성분 분석 본문
- 주성분 분석
주성분 분석이란 고차원의 데이터를 저차원의 데이터로 차원 축소하는 알고리즘입니다. 주로 고차원의 데이터를 3차원 이하의 데이터로 바꿔서 시각화 하는데 많이 사용되며 유용한 정보만을 살려서 적은 메모리에 저장하거나 데이터의 노이즈를 줄이고 싶을때도 사용되는 알고리즘입니다.
먼저 주성분 분석의 작동원리에 대해 알아보겠습니다. 이해하기 쉽게 시각화 가능한 2차원의 데이터를 1차원의 데이터로 축소하는 과정을 알아보겠습니다. 아래는 2차원의 데이터입니다.

위 데이터를 1차원으로 변경하기 위해 x1 좌표로 옮겨보겠습니다.

x1 좌표로 옮기게되면 1차원으로 됬긴하지만 많이 중첩되어 데이터를 구분하기 어려워진 것을 눈으로 확인할 수 있습니다. 그러면 x2는 어떨까요?

x2 좌표로 옮겨도 동일한 것을 알 수 있습니다. 그렇다면 어떻게하면 데이터가 하나도 중첩되지 않게 할 수 있을까요? 데이터 정보의 유실이 가장 적은 선을 찾아내어 그 선에 사영하면 됩니다.
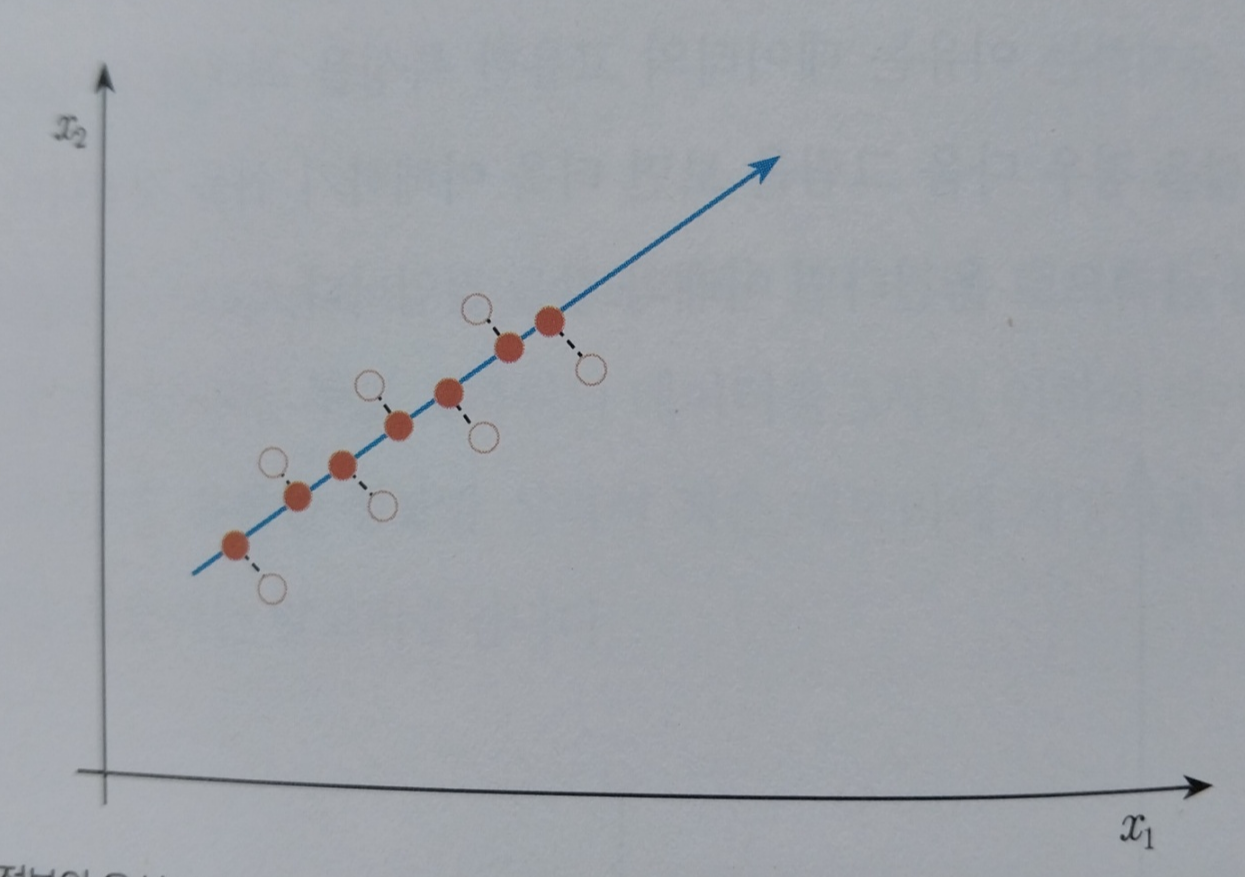
위 사진처럼 데이터의 유실이 가장 적은 선을 찾아내어 사영하게되면 데이터의 중첩없이 데이터를 볼 수 있습니다.
데이터의 중첩이 가장 적다는 말은 데이터의 분산이 가장 크다는 말과 동일합니다.
주성분 분석은 분산이 가장 큰 차원을 찾아내어 차원을 축소합니다. 이때 분산이 가장 큰 차원은 수학적으로 공분산 행렬에서 고윳값이 가장 큰 고유백터라고 합니다.
만약 데이터가 5차원이고 2차원으로 데이터의 차원을 줄이고 싶다면 마찬가지로 주성분 분석 알고리즘은 공분산 행렬에서 고윳값이 큰 순서대로 고유백터를 정렬한 후 가장 큰 고유 벡터와 큰 고유 벡터를 축으로 2차원 데이터를 만들면됩니다.
- 고차원의 식습관 데이터를 차원 축소후 시각화 실습
고차원의 식습관 데이터를 주성분 분석으로 차원 축소하여 시각화 해보겠습니다. 먼저 데이터를 만들어줍니다.
df = pd.DataFrame(columns=['calory', 'breakfast', 'lunch', 'dinner', 'exercise', 'body_shape'])
df.loc[0] = [1200, 1, 0, 0, 2, 'Skinny']
df.loc[1] = [2800, 1, 1, 1, 1, 'Normal']
df.loc[2] = [3500, 2, 2, 1, 0, 'Fat']
df.loc[3] = [1400, 0, 1, 0, 3, 'Skinny']
df.loc[4] = [5000, 2, 2, 2, 0, 'Fat']
df.loc[5] = [1300, 0, 0, 1, 2, 'Skinny']
df.loc[6] = [3000, 1, 0, 1, 1, 'Normal']
df.loc[7] = [4000, 2, 2, 2, 0, 'Fat']
df.loc[8] = [2600, 0, 2, 0, 0, 'Normal']
df.loc[9] = [3000, 1, 2, 1, 1, 'Fat']
칼로리, 아침, 점심, 저녁, 운동과 몸의 체형과의 관계를 나타내고 있습니다. 이때 5개의 데이터로 몸의 체형의 관계를 나타내고 있습니다. 이를 시각화 하게되면 6차원이 되므로 눈으로 보기어렵기떄문에 간단히 1차원으로 시각화해보겠습니다.
먼저 데이터를 전처리해줍니다.
X = df[['calory', 'breakfast', 'lunch', 'dinner', 'exercise']]
Y = df[['body_shape']]
그리고 칼로리의 경우 데이터가 너무 크기때문에 정규화 작업을 해줍니다.
from sklearn.preprocessing import StandardScaler
x_std = StandardScaler().fit_transform(X)
이제 공분산 행렬을 구하고 고유값과 고유벡터를 구해보겠습니다.
import numpy as np
features = x_std.T
covariance_matrix = np.cov(features)
print(covariance_matrix)
eig_vals, eig_vecs = np.linalg.eig(covariance_matrix)
위 고유벡터에대한 고윳값은 아래 코드로 확인가능합니다.
print('\nEigenvalues \n%s' %eig_vals)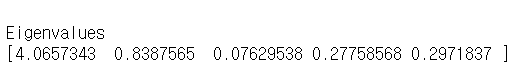
첫번째 고유 벡터의 고윳값이 가장 큰것을 확인할 수 있습니다.
이제 첫번쨰 고유 벡터로 사영시켜보겠습니다.
#사영
projected_X = x_std.dot(eig_vecs.T[0]) / np.linalg.norm(eig_vecs.T[0])
#시각화
result = pd.DataFrame(projected_X, columns=['PC1'])
result['y-axis'] = 0.0
result['label'] = Y
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.lmplot('PC1', 'y-axis', data=result, fit_reg=False, # x-axis, y-axis, data, no line
scatter_kws={"s": 50}, # marker size
hue="label") # color
# title
plt.title('PCA result')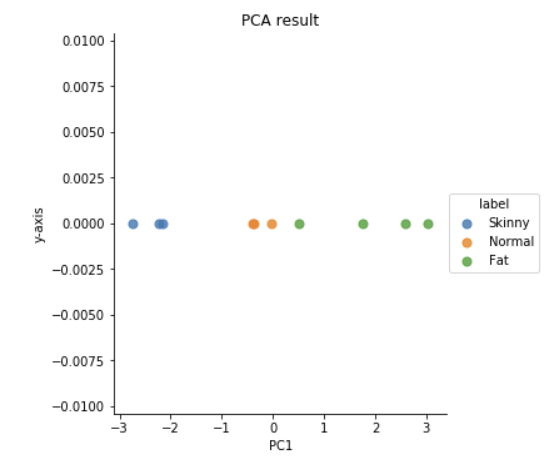
PC1이라는 5가지 변수의 총합으로 몸의 체형을 구분하는 1차원 데이터로 변환되었습니다.
- 사이킷런으로 더 쉽게 사용
사이킷런을 사용하면 코드를 획기적으로 줄일 수 있습니다.
from sklearn import decomposition
pca = decomposition.PCA(n_components=1)
sklearn_pca_x = pca.fit_transform(x_std)
sklearn_result = pd.DataFrame(sklearn_pca_x, columns=['PC1'])
sklearn_result['y-axis'] = 0.0
sklearn_result['label'] = Y
sns.lmplot('PC1', 'y-axis', data=sklearn_result, fit_reg=False, # x-axis, y-axis, data, no line
scatter_kws={"s": 50}, # marker size
hue="label") # color
위 코드 실행시 시각화를 바로할 수 있습니다.
'AI > machine-learning' 카테고리의 다른 글
| 지도 학습 - 퍼셉트론 실습 (1) | 2023.11.17 |
|---|---|
| 지도 학습 - 딥러닝 (0) | 2023.11.16 |
| 비지도 학습 - 로지스틱 회귀 (0) | 2023.11.07 |
| 비지도학습 - 선형 회귀 (1) | 2023.11.06 |
| 비지도학습 - 군집화 (0) | 2023.11.04 |




